Posted on 2016/01/24, 10:57 PM By admin22
カルマンフィルタという、誤差のある観測データから真の値を推測する手法を、Playgroundでテストしてみました。
参考:
http://sinhrks.hatenablog.com/entry/2014/11/01/231333
http://scipy.github.io/old-wiki/pages/Cookbook/KalmanFiltering
http://www.sat.t.u-tokyo.ac.jp/~omi/random_variables_generation.html#Gauss
環境: Xcode 7.2 / Mac OSX 10.10.5
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
import UIKit let n = 300 let Q = 1e-5 let R = pow(0.1, 2) var xhat = [Double](count: n, repeatedValue: 0) var xhatminus = [Double](count: n, repeatedValue: 0) var P = [Double](count: n, repeatedValue: 0) var K = [Double](count: n, repeatedValue: 0) var Pminus = [Double](count: n, repeatedValue: 0) func norm(x:Double, _ mu:Double, _ si:Double) -> Double{ return 1.0 / sqrt(2 * M_PI * si) * exp(-0.5 * (x - mu) * (x - mu) / si) } for var d = -2.0; d < 2.0; d += 0.1 { norm(d, 0, 1.0) norm(d, 0, 0.2) norm(d, 1, 0.2) } func rand() -> Double { return Double(arc4random_uniform(1000) + 1) / Double(1000 + 2) } func rand_normal(mu: Double, _ si: Double) -> Double { let z:Double = sqrt( -2.0 * log(rand()) ) * sin( 2.0 * M_PI * rand() ); return mu + si * z; } var max = 0.0 var min = 1.0 var h = [Int](count: 10, repeatedValue: 0) var z:[Double] = [] let TrueValue = 3.0 for _ in 0..<n { let r = rand_normal(TrueValue, 1.0) if r > max { max = r } if r < min { min = r } z.append(r) if r < -3 { h[0] += 1 } else if -3 <= r && r < -2 { h[1] += 1 } else if -2 <= r && r < -1 { h[2] += 1 } else if -1 <= r && r < 0 { h[3] += 1 } else if 0 <= r && r < 1 { h[4] += 1 } else if 1 <= r && r < 2 { h[5] += 1 } else if 2 <= r && r < 3 { h[6] += 1 } else if 3 <= r && r < 4 { h[7] += 1 } else if 4 <= r && r < 5 { h[8] += 1 } else if 5 <= r { h[9] += 1 } } print("max: \(max) min: \(min)") print(h) for k in 1..<n { xhatminus[k] = xhat[k-1] Pminus[k] = P[k-1] + Q K[k] = Pminus[k] / (Pminus[k] + R) xhat[k] = xhatminus[k] + K[k] * (z[k] - xhatminus[k]) P[k] = (1 - K[k]) * Pminus[k] } |
実行結果
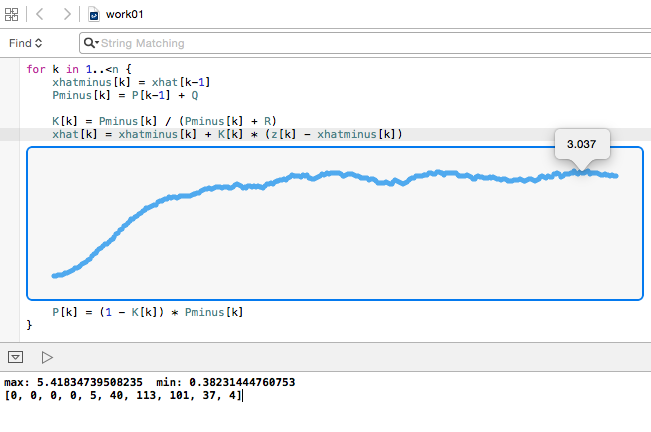
途中、rand_normalのばらつき具合をテストしています。rが真値3.0を中心にばらついてることを確認できました。(下部Windowのprint出力)
ばらつきを持ったデータ列zから推定されて、真値3.0に近づいていく様子がグラフで見られます。
Categories: 未分類 タグ: Swift
