エドワード・フレンケル「数学の大統一に挑む」(Love and Math -The Heart of Hidden Reality-)の中で語られているある数式にとても興味を持ち、プログラムによって確認してみました。
ハリウッド俳優のようなルックスの著者は、数学の教授で、NHKの白熱教室でもこの数式に関してとても興奮して語っていたのがとても印象的でした。
フェルマーの最終定理の証明することとなった、志村・谷山・ヴェイユ予想はラングランズ・ブログラムの特殊ケースといわれ、ある方程式を解くことで、その不思議なつながりを体験することができると解釈しました。
番組ではこの日本人数学者のエピソードも語られ、その偉大さを初めて知りました。

演算に関してだけ簡単に説明すると、

y^2 + y = x^3 – x^2

この方程式と

q * (1-q)^2 * (1-q^11)^2 * (1-q^2)^2 * (1-q^22)^2 * (1-q^3)^2 * (1-q^33)^2 * (1-q^4)^2 * (1-q^44)^2 …..

という規則性のある式は、元々全く関係のないものですが、前者の式の解の個数と後者の式を展開した時の係数が一致するというものです。
プログラムでは、前者を素数を法とする数で総当たりに解を導きます。後者は数式を展開し係数を取得します。
前者は、数が大きくなればなるほど、計算コストがかかるのに、後者はそれを数式の展開という形で導き出してしまう、ということがとても不思議な部分です。
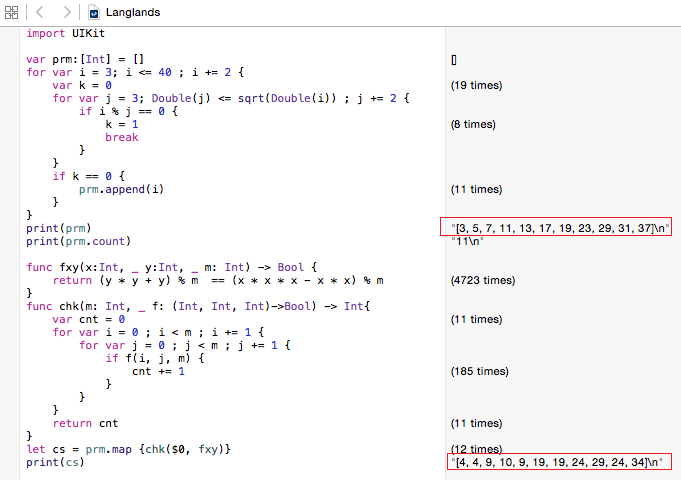
前者はSwiftで、後者はOctaveで計算しました。

Swiftでは、まず素数列を取得しそれから各素数に対して、方程式を解きます。
素数から解の個数を引いた値と、Octaveで演算した素数番目の係数と見比べます。

素数
3,5,7,11,13,17,19,23,29,31,37

解の個数
4,4,9,10,9,19,19,24,29,24,34

(素数)-(解の個数)
-1,1,-2,1,4,-2,0,-1,0,7,3

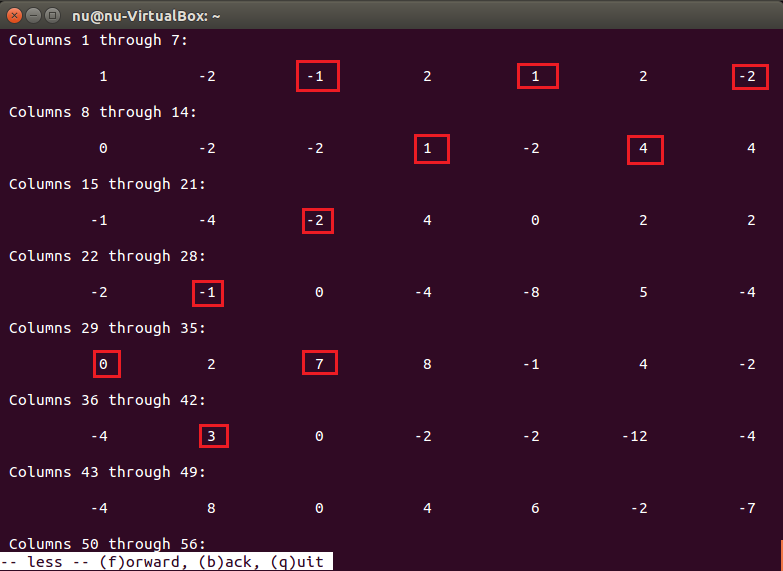
Octaveでは、

このプログラムにより、係数だけの演算をします。insz関数はゼロを配列の真ん中に挿入しています。
[1 1] -> x + 1
[1 0 1] -> x^2 + 1
[1 0 0 1] -> x^3 + 1
といった具合です。

しくみがシンプルなだけにこの結果に驚かされます。
このような現象が、まだまだたくさん隠されているということなのでしようね。
– Hidden Reality –

(数学者って憧れます)