1/fゆらぎというのが、ちょっと前にはやりましたが、私が一番最初に知ったのは、それよりも随分前1981年に出版された「マイコン・サウンド学入門」(マイクロコミュニケーションズ)という本でした。そこにホワイトノイズを積分すると、ブラウンノイズに、1/2階積分するとピンクノイズになるという実験があり、とても興味をひかれました。ホワイトノイズがランダム1/(f^0)、ブラウンノイズが1/(f^2)、そしてピンクノイズが1/fゆらぎに相当します。
この本では、1/fゆらぎ自動作曲機をアセンブラで記述されたプログラムあり、音が聞けるようにフォノシートがありと、当時とても衝撃的な内容でした。「音楽と数学」をより深く考えるきっかけとなった貴重な本です。

ふとしたことからこの本を見つけ、当時理解したつもりでいた、ホワイトノイズの1/2階積分を実際にテストしてみようと思いました。
前回、1/2階積分の計算方法は、この本を参考にしています。(同じではないですが・・)

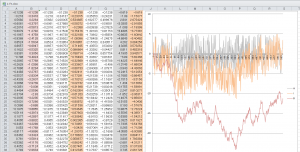
上記、まず512個のランダム数(A列)を順にたしたもの(積分)をブラウンノイズ(B列)、それを前回の数値フィルタで1/2階積分したものが(E列)を示します。(係数をソルバーで決めるときに最小二乗法で直線をフィットしますが、元のデータができるだけ直線になるように係数1を決め、それから係数2をあてはめたりして調整します。) 値をとる振幅が小さすぎたので、(A)(B)を5倍にしたものを(H)(I)としました。
ランダムとブラウン運動との中間に、1/fゆらぎがあるように見えます。

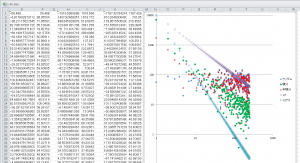
次に、パワースペクルトを求めるため(H)(B)(I)をそれぞれフーリエ解析したものが、次の図の(E)(H)(K)、それぞれ複素数の絶対値IMABS()をとったのが、(F)(I)(L)になります。表示対象は、対称性があるので半分の256サンプルにします。

ブロットされたものを見ると、ランダムは水平に分布(1/f^0)し、半積分されたものは、右下に傾いて分布、積分されたものは、さらに傾いて分布しているように見えます。1/f,1/f^2の傾きと比較していみると、積分と半積分、どちらが近いかといえば、積分は1/f^2、半積分は1/fになります。

もっとデータ数をふやせば、精度もあがるかもしれません。