宇宙際タイヒミュラー(IUT)理論。「ABC予想」問題を解くカギとして京都大学の望月 新一氏が発表されたものです。
これについて解説した、加藤文元氏の「宇宙と宇宙をつなぐ数学-IUT理論の衝撃」(角川書店)を書店で見たとき興味があったので購入しました。
最近、数学の難問「ABC予想」を証明したという望月氏の600ページもある論文の査読が完了した、というニュースにより、この書籍を再度読み直して盛り上がっているとこうです。これが本当だとかなりすごいことになるようです。
http://www.kurims.kyoto-u.ac.jp/~motizuki/papers-japanese.html

「ABC予想」についてはWikipediaから。
https://ja.wikipedia.org/wiki/ABC%E4%BA%88%E6%83%B3

a + b = c
を満たす、互いに素な自然数の組 (a, b, c) に対し、積 abc の互いに異なる素因数の積を d と表す。このとき、任意の ε > 0 に対して、
c > d^(1+ε)
を満たす組 (a, b, c) は高々有限個しか存在しないであろうか？

εが0のときは無限にあるが、0よりも少しで多い場合(0.000000000001でも)、有限になるというものです。この数が大きくなるほど発見がしづらくなります。Wikipediaにその分布があります。
ここではその計算する手段だけでもと思い、数学関数に強いJuliaを使って計算してみました。
ここではεが0でどのような分布をしているのか、大小関係はどうなのか、を見てみたいと思います。

環境はMacのコマンドラインからREPLを起動して、そこにペーストしました。
(jupyter notebookの環境でもいいのですが、できるだけシンプルに起動するため。本当はファイル実行したかったのですが、plotがうまくいかなかった。)

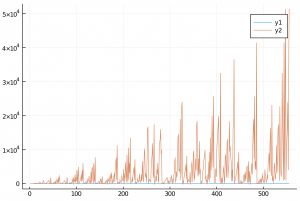
y1がc、y2がdに相当。

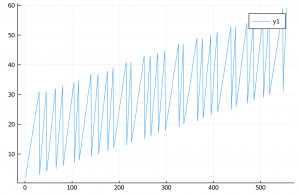
y1のみ表示。

互いに素の組み合わせを30 x 30にしましたが、本当はもっと大きな数が好ましいです。
すぐにレンジオーバーしてしまうので、本格的にやるのなら、mpfrライブラリのようなものを使う必要があります。

https://decode.red/blog/tag/mpfr/

書籍の「対称性通信」の章に、

「たし算とかけ算の絡み合い」を解いて、その間の関係を明らかにすることこそ、数の世界の深奥の秘密の一端を明らかにする・・

とあります。単純なものほどその本質を説明すのが難しいということなのかもしれません。
素数出現の規則性をまだ見いだせないのもそうですが、そもそも掛け算というのは足し算の拡張ではないのではないかとか、いろいろと想像が膨らみます。
この理論の今後の展開がとても楽しみです。

ここでは、最大公約数、素因数分解、根基(Radical)といったものをJuliaでコーディングする手軽さを味わえて有意義でした。