今年初めは、量子コンピュータにチャレンジです。C言語で簡単な演算をシミレートしてみました。
参考)
CQ出版「インターフェイス」(2019/3)
インプレス「いちばんやさしい量子コンピュータの教本」
インターフェイス誌はちょっと前のものになっていますが、C言語による説明が書かれているのでそれを参考にしました。演算の考え方については量子コンピュータ教本の量子アルゴリズムを参考にしました。
環境)
https://godbolt.org/
量子コンピュータの考え方は、他を参考にしていただいて、下記は量子ビットが重ね合わせ状態になるアダマールゲートの図です。
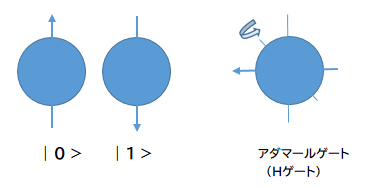
この重ね合わさった状態では、0と1が50%の確率で出現します。
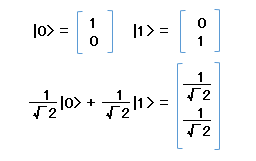
(1/√2は、三角関数のサイン/コサイン45度の値)
ベクトルで表現された2量子ビットを使い、片方にHゲート、もう片方にCNOTゲートを使って演算します。
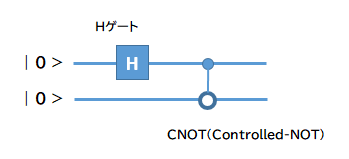
(黒丸:制御量子ビット 白丸:ターゲット量子ビット 制御が1のときターゲットを反転)
まずは、Cで複素数が使える環境の確認と、演算結果を確率で表示する関数の確認です。
答えが確率によって毎回変わるのは、普通の考え方では使えないのですが、答えを絞りこむことはできます。
(今回、これを実装してみたかった)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <stdio.h> #include <stdlib.h> #include <complex.h> #include <math.h> int measure(double complex c){ int ret; double r = (double)rand()/(double)0x7fffffff; double a = pow(cabs(c), 2.0); if(r < a){ ret = 0; } else{ ret = 1; } return ret; } int main(void) { double complex q; int q1[2], q2[2], a0=0, a1=0, a2=0, a3=0; q2[0] = 0; q2[1] = 1; q = 1.0/sqrt(2) + 0.0i; for(int i=0;i<10;i++){ int ret; ret = measure(q); q1[0] = ret; q1[1] = ret==1?0:1; q2[0] = ret==1?1:0; q2[1] = q2[0]==1?0:1; printf("%d %d %d %d \n", q1[0], q1[1], q2[0], q2[1]); if(q1[0] == 0 && q2[0] == 0) a0 ++; if(q1[0] == 0 && q2[0] == 1) a1 ++; if(q1[0] == 1 && q2[0] == 0) a2 ++; if(q1[0] == 1 && q2[0] == 1) a3 ++; } printf("Answer: %d %d %d %d\n", a0, a1, a2, a3); return 0; } |

(演算の評価(観測)は最後にやるべきですが、簡単にするためHゲートの後にやっています。)
量子ビットq1,q2の値をベクトルで表現しています。[0]と[1]は反するものとして表現しています。
量子ビットの値としては[0]になります。
2bitのとりうるすべて値(00,01,10,11)の出現数をカウントしました。
すると、00と11のみとなります。量子のもつれによる結果の絞り込み、というそうです。
他にもさまざまなアルゴリズムがありますが、Cで実装するにはかなり難しくなります。
今後は他の言語やツールを使って試してみる予定です。
まずは第一歩でした。