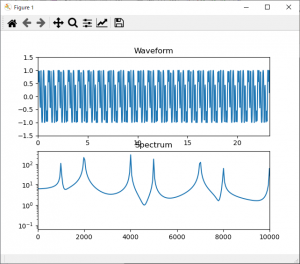
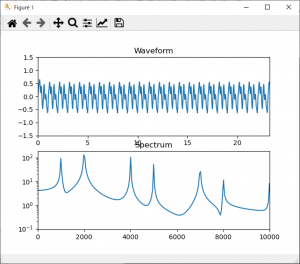
電子工作、制御系、電気回路などあらゆるところで出てくるローパスフィルタ。信号の種類によってさまざまな用途がありますが、ここでは前々々回FM音源を鳴らしたときの音を使って試してみました。
ずっと前に伝達関数で表現される一次遅れというものをOctaveを使って表示したことがありました。
これと全く同じことをPythonを使って音波形に施してみるのが目的です。
なぜ遅れることがローバスフィルタになるのかと最初はよくわかりませんでした。たくさんの周波数成分を含んだ波形だとわかりやすいのですが、高い周波数ほど遅れたときの位相ずれが大きいことから、打ち消しあいが起き、それにより小さくなってしまうので減衰するということのようです。(周波数の違うサイン波形を横にならべるとわかりやすいです)
まずは一次遅れの伝達関数からボート線図をプロットしました。
参考: https://gsmcustomeffects.hatenablog.com/entry/2019/01/13/112150
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np from scipy import signal import matplotlib.pyplot as plt num = [1] den = [1000 * 0.000_001, 1] #1kΩ 1uF s = signal.lti(num, den) w, mag, phase = signal.bode(s) f = w/(2.0*np.pi) fig, (ax0, ax1) = plt.subplots(nrows=2, sharex=True) ax0.semilogx(f, mag, 'b-') ax0.set_ylabel("Magnitude[dB]") ax1.semilogx(f, phase, 'r-') #ax1.plot(f, phase) ax1.set_ylabel("Phase[degree]") ax1.set_xlabel("Freq[Hz]") plt.show() |
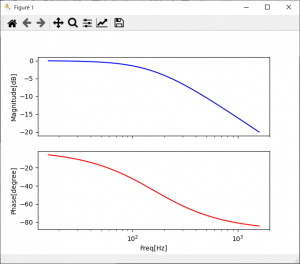
特性を確認した上で、このシステムを使って上記FM音源のソースをもとに、FM音源のフィルタをシミュレートしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
import sys import numpy as np import pyaudio import struct import cv2 import threading import time import matplotlib.pyplot as plt import scipy.signal as sg RATE=44100 bufsize = 32*1024 keyon = 0 velosity = 0.0 num = [1] den = [100000*0.000_001, 1] system = sg.lti(num, den) def fm(t): wave = np.sin(2.0*np.pi*t + b * np.sin(2.0*np.pi*t*r)) return wave x=np.arange(bufsize) pos = 0 pitch = 1000 filter = 0 #フィルタのOn/Off playing = 0 def audioplay(): global pos,velosity p=pyaudio.PyAudio() stream=p.open(format = pyaudio.paInt16, channels = 1, rate = RATE, frames_per_buffer = bufsize, output = True) while stream.is_active(): t = pitch * (x+pos) / RATE pos += bufsize wave = fm(t) if(filter == 1): t_out, v_out, xx = sg.lsim(system, wave, t) wave = v_out if keyon == 1: velosity = 1.0 else: velosity = 0.0 buf = velosity * wave buf = (buf * 32768.0).astype(np.int16) #16ビット整数に変換 buf = struct.pack("h" * len(buf), *buf) stream.write(buf) if playing == 0: break stream.stop_stream() stream.close() p.terminate() if __name__ == "__main__": if len(sys.argv) != 3: print("<command> <b> <r>") exit(1) b = float(sys.argv[1]) #モジュレータ振幅:変調指数 今回は2 r = float(sys.argv[2]) #キャリアモジュレータ周波数比 今回は3 thread = threading.Thread(target=audioplay) thread.start() sampleN = 1024 t0 = pitch * np.arange(sampleN) / RATE t = t0 wave = fm(t) if(filter == 1): t_out, v_out, xx = sg.lsim(system, wave, t) wave = v_out Spectrum = abs(np.fft.fft(wave)) frq = np.fft.fftfreq(sampleN,1.0 / RATE) plt.clf() plt.subplot(2,1,1) plt.title("Waveform") plt.plot(t0, wave) plt.xlim([0,pitch * sampleN / RATE]) plt.ylim([-1.5, 1.5]) plt.subplot(2,1,2) plt.title("Spectrum") plt.yscale("log") plt.plot(frq[:int(sampleN/2)],Spectrum[:int(sampleN/2)]) plt.xlim([0,10000]) plt.pause(1) keyon = 1 time.sleep(1) keyon = 0 playing = 0 cv2.destroyAllWindows() |
プロット結果から差異が明確にあらわれました。音はわかりづらいですが、若干こもった感じになりました。
また伝達関数で設定している抵抗値とキャパシタの容量が正しいかどうか、LTspiceで確認しました。

1kHzで-20dbまで減衰しているので、最初のボード線図と一致してそうです。
ノイズ対策などでローバスフィルタが使われますが、フィルタというと削るということで消極的処理のように感じますが、楽器のシンセサイザーの世界では、音に特徴(クセ)をもらたす大事な役割を果たします。
モーグシンセやRoldand TB-303のようなクセがスゴい二次遅れ系のフィルタについても、作れたらいいなぁと思っているこのごろです。