デジタルシンセサイザのFM音源について、以下サイトを参考に動かしてみました。
「Pythonで学ぶシンセサイザー」
https://qiita.com/a2kiti/items/4449d15e16c1793fd53f
このサイトでは、エンベロープやフィルタ、ディレイまで実装されていて、本当に素晴らしいです。
私はUIの部分を省略して、FMの波形表示と音を出す最小限の部分を実装しました。
これをみるとPythonによってかなりシンプルに実現できることが実感できます。
FM音源というと、YAMAHAのシンセサイザDXシリーズの音源で、その後PCやゲーム機に幅広く採用されました。
なんといってもシンプルな実装で複雑な波形を表現できることが大きな特徴です。
A*sin(2*pi*fc*t + B*sin(2*pi*fm*t))
A:キャリア振幅
fc:キャリア周波数
B:変調指数(モジュレータ振幅)
fm:モジュレータ周波数
t:時間
YAMAHA DX7ではオペレータが6つあり様々な組み合わせで32種類のバリエーションを持っていますが、
ここでは最小単位の2オペレータ(sin関数が二つ、入れ子になっている構造)で、コマンドからパラメータを変えながら、音と波形を確認するプログラムを作りました。
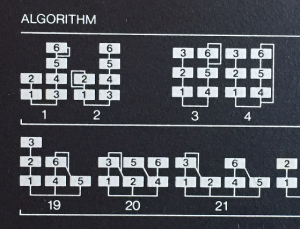
DX7のアルゴリズムの一部。アルゴリズム1のオペレータ1(キャリア),2(モジュレータ)、この部分だけ切り取った形に相当します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
import sys import numpy as np import pyaudio import struct import cv2 import threading import time import matplotlib.pyplot as plt RATE=44100 bufsize = 32 keyon = 0 pre_keyon = 0 pitch = 440 velosity = 0.0 b = 1.0 r = 1.0 def fm(t): wave = np.sin(2.0*np.pi*t + b * np.sin(2.0*np.pi*t*r)) return wave x=np.arange(bufsize) pos = 0 playing = 1 def audioplay(): global pos,velosity p=pyaudio.PyAudio() stream=p.open(format = pyaudio.paInt16, channels = 1, rate = RATE, frames_per_buffer = bufsize, output = True) while stream.is_active(): #位相計算 t = pitch * (x+pos) / RATE t = t - np.trunc(t) pos += bufsize wave = fm(t) if keyon == 1: velosity = 1.0 else: velosity = 0.0 buf = velosity * wave buf = (buf * 32768.0).astype(np.int16) #16ビット整数に変換 buf = struct.pack("h" * len(buf), *buf) stream.write(buf) if playing == 0: break stream.stop_stream() stream.close() p.terminate() if __name__ == "__main__": if len(sys.argv) != 3: print("<command> <b> <r>") exit(1) b = float(sys.argv[1]) #モジュレータ振幅:変調指数 r = float(sys.argv[2]) #キャリアモジュレータ周波数比 thread = threading.Thread(target=audioplay) thread.start() sampleN = 1024 t0 = pitch * np.arange(sampleN) / RATE t = t0 - np.trunc(t0) wave = fm(t) Spectrum = abs(np.fft.fft(wave)) frq = np.fft.fftfreq(sampleN,1.0 / RATE) plt.clf() plt.subplot(2,1,1) plt.title("Waveform") plt.plot(t0, wave) plt.xlim([0,pitch * sampleN / RATE]) plt.ylim([-1.5, 1.5]) plt.subplot(2,1,2) plt.title("Spectrum") plt.yscale("log") plt.plot(frq[:int(sampleN/2)],Spectrum[:int(sampleN/2)]) plt.xlim([0,10000]) plt.pause(1) time.sleep(1) keyon = 1 pitch = 440 time.sleep(1) keyon = 0 playing = 0 cv2.destroyAllWindows() |
環境:Python3.7/Anaconda/Windows10
音の再生のためのライブラリpyaudioのインストールはここを参考させていただきました。(watlab-blog.com/2019/05/21/pyaudio-install/)
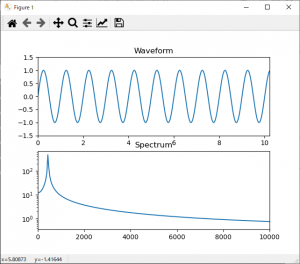
まずは基本波形で、b=0, r=1
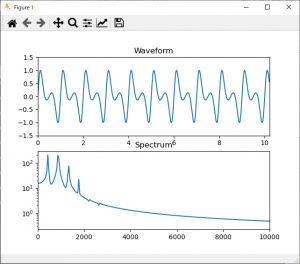
b=1.3, r=1
b=1.3, r=1.9
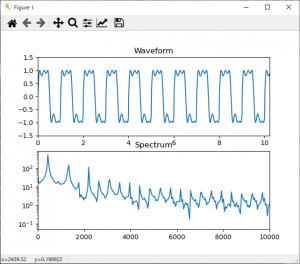
わずかな変化でも、だんだん複雑な音になっていきます。
実際のシンセでは時間的変化(エンベロープジェネレータ)の効果が各オペレータにかかるので、かなり複雑な変化を作ることができます。FM音源の難しさはここにあります。
FM音源は、一時飽きられた感がありましたが、最近また操作性の改善や、簡単に非整数次倍音を実現できる特徴(効果音的な過激な用途に有用)からまた見直されているようです。
私はリアルな音よりも、リアルに近い音から他の音に連続的に変化できるところが魅力だと思っています。
演算で波形をつくるというと、フーリエ級数が思い浮かびますが、比較すると計算量が少ないことがよくわかります。位相変調というしくみが、少ない演算コストで複雑な波形(豊かな倍音)を実現しています。
なによりPythonで、ここまでできてしまうことに驚きでした。通常のデータ処理と考えれば当然ですが、新たなシンセアルゴリズムつくるのにいい環境です。
