Posted on 2020/03/14, 11:54 AM By admin22
「大きさ」と「向き」の二つの量をもつベクトル。3Dグラフィックを扱うとき必ず出てきますが、もう少し勉強しようと数学のベクトル解析という分野を学び始めました。
しかし数式ばかりでなかなか学んだ感が得られなかったので、ベクトル場という部分について理解を深めるために、Processingでプログラムを作ってみました。
参考) https://medium.com/@vladisluka/vector-fields-in-processing-779516b15141
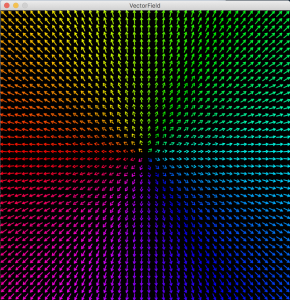
上が基本的なベクトル関数
→f = (x, y)
の例。
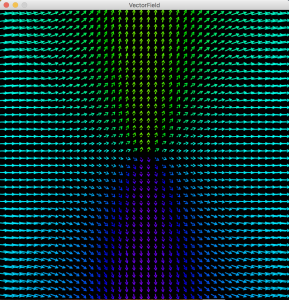
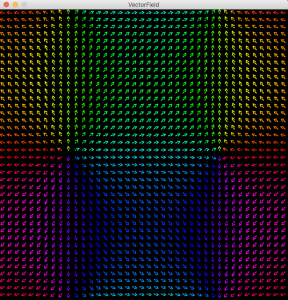
Cellを作り、Cell単位でベクトルを表現しています。
「大きさ」は長さとしてCellに入る程度に丸めています。また「向き」によって色を変えてます。
こうやってみると「向き」というのは情報量が多いことが実感できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
int len = 16; void setup () { size(640, 640); background(0); colorMode(HSB, 360); int cols = floor(width / len); int rows = floor(height / len); for (int i = 0; i < cols; i++) { for (int j = 0; j < rows; j++) { Cell cell = new Cell(i, j); pushMatrix(); strokeWeight(2); stroke(degrees(cell.arg)+180, 360, 360); translate((i + 0.5) * len, (j + 0.5) * len); rotate(cell.arg); line(cell.mag*2, 0, -cell.mag*2, 0); translate(len/2, 0); float a = radians(150); float x1 = 5 * cos(a); float y1 = 5 * sin(a); line(0, 0, x1, y1); line(0, 0, x1, -y1); popMatrix(); } } } class Cell { float arg; float mag; Cell (int i, int j) { float x = (i + 0.5) * len; float y = (j + 0.5) * len; x = map(x, 0, width, -3, 3); y = map(y, 0, height, -3, 3); //float u = x; //float v = y; //float u = x * x; //float v = 0.5 * y; float u = cos(x); float v = sin(y); PVector vec = new PVector(u, v); mag = vec.mag(); arg = vec.heading(); } } |
様々なデータの可視化にも有用ですが、コンピータグラフィックを使ったアートにも威力を発揮しそうです。
Categories: Graphics タグ: Processing