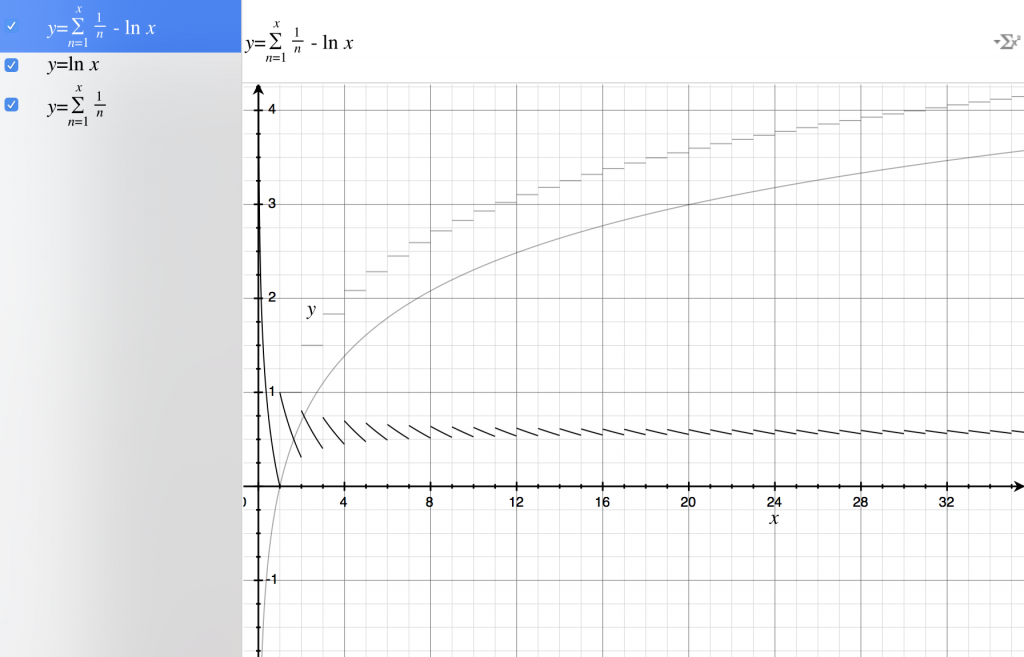
オイラー定数γ。円周率π,ネイピア数e,虚数単位iにつぐ数学界で重要な定数といわれています。
発散する調和級数からlog(x)を引くと収束する値γになり、まだ超越数なのか無理数なのかもわかっていない不思議な数のようです。
イメージしやすいように、MacのユーティリティGrapherで表示してみました。
実際に計算するため、またMPFRを使ってみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include <stdio.h> #include <stdlib.h> #include <gmp.h> #include <mpfr.h> int main() { mpfr_t r, one, work, nn, sum; mpfr_init2(r, 100); mpfr_init2(one, 100); mpfr_init2(nn, 100); mpfr_init2(work, 100); mpfr_init2(sum, 100); unsigned int x = 3000000000; mpfr_set_ui(one, 1, MPFR_RNDD); mpfr_set_ui(sum, 0, MPFR_RNDD); for(unsigned int i=1;i<=x;i++){ mpfr_set_ui(nn, i, MPFR_RNDD); mpfr_div(work, one, nn, MPFR_RNDD); mpfr_add(sum, sum, work, MPFR_RNDD); } mpfr_log_ui(work, x, MPFR_RNDD); mpfr_sub(r, sum, work, MPFR_RNDD); mpfr_out_str(stdout, 10, 0, r, MPFR_RNDD); mpfr_clear(r); } |
Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E3%81%AE%E5%AE%9A%E6%95%B0
では、
およそ0.57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 35988 05767 23488 48677 26777 66467 09369 47063 29174 67495…
とありますが、このブログラムの結果は
5.7721566506819952722608849107166e-1
real 3m8.076s
user 3m7.427s
sys 0m0.585s
となり、そこそこ標準的なPCでこれだけ時間をかけて小数点第8位までしか一致しませんでした。
なかなか収束が遅いようです。
オイラーが6位まで計算したとのことですが、PCのない時代にすごいです。
現代数学のホットな研究対象であるゼータ関数論との関係も深いこの定数ですが、この分野に何か惹きつけられるものがあり勉強中です。こういうときプログラム言語というのは理解を深めるためにとても役に立つと実感します。
最近のPCの性能のおかげで、数学のミステリーに迫る楽しみを味わえるのは、いい時代です。