素粒子のようなミクロの世界、宇宙のようなマクロの世界など、複素数の不思議な性質が様々な場面で使われています。関連書籍を読んでいて、もしかしたらこの世界の根本的な原理を表現するのに不可欠なものなのではと、もっと勉強したくなりました。その入り口として複素関数による写像がとっつきやすく、見た目も面白いので試してみました。
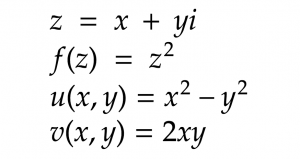
(https://www.mathcha.io/editor 利用)
複素数平面x,yで表されるzを、演算結果の実数部、虚数部をわけてu,v平面に変換します。
シンプルな複素数の二次関数ですが、これが取りうる値の空間をグラフ表示してみました。
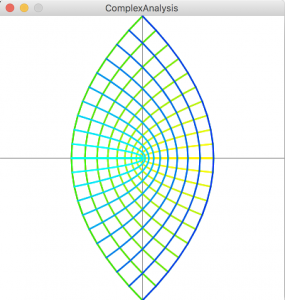
上図(u,v)は下図(x,y)のとりうる領域を変換したものです。
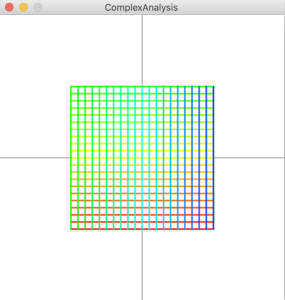
これら、(u,v)の方が実際にはもっと大きくなりますが、座標を調整したあります。
(u,v)のどの部分が(x,y)のどの部分と対応するかわかりやすくするために色を赤から青に変化させてみました。
これを順に見ていくと(u,v)の方には後半の半分しかないことがわかります。これは重複して描画しているからです。(領域が重なる)
もう少しシンプルにするため横線のみの描画をしてみました。
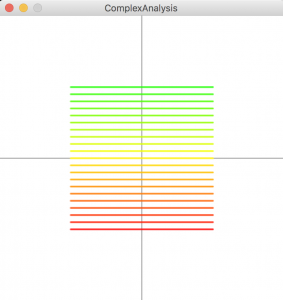
これを変化したのが下です。
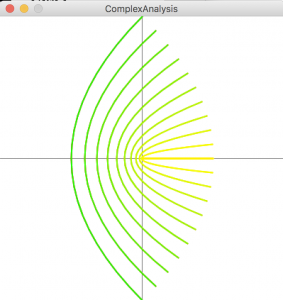
下のコードは一番上の画像を出力したものです。
vertexの部分のコメントを切り替えると、変換前後の画像の切り替えができます。いろいろと描画単位を変えてみると理解が深まります。
ところどころコメントがされていますが、線を一本一本アニメーションして描画することにも対応しました。(コードを短くするためこのようにしました。手抜きともいいます^^)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
void setup() { size(400, 400); frameRate(10); } int f = -10; void draw() { background(255); strokeWeight(1); stroke(127); line(width/2, 0, width/2, height); line(0, height/2, width, height/2); noFill(); strokeWeight(2); pushMatrix(); translate(width/2, height/2); colorMode(HSB); f = 10; int c = 0; for(int y=-10;y<=f;y++){ beginShape(); stroke( c, 255, 255); for(int x=-10;x<=10;x++){ //vertex(x*10, -y*10); int u = x * x - y * y; int v = 2 * x * y; vertex(u, v); } endShape(); c += 4; } for(int x=-10;x<=f;x++){ beginShape(); stroke( c, 255, 255); for(int y=-10;y<=10;y++){ //vertex(x*10, -y*10); int u = x * x - y * y; int v = 2 * x * y; vertex(u, v); } endShape(); c += 4; } popMatrix(); f ++; if(f == 10){ // f = -10; } } |
空間が曲げられる様子が面白いです。シンプルな二次関数でもこれですから、もっといろいろと期待できます。Processingはこういうことにとても便利ですね。(学生時代にあったら・・)
