Posted on 2017/12/30, 9:57 AM By admin22
数学では四元数といわれ、虚数のi,j,kを三つ使い表現されとても難しく感じるものですが、3Dグラフィックスの世界では、3D空間のオブジェクトの回転でなくてはならない考え方です。X,Y,Z軸それぞれで回転するのではなく、あるベクトルを軸としてその周りを回転します。天体望遠鏡を持っている人なら、赤道儀のしくみからイメージしやすいかもしれません。
前回Processingで3D空間のテストをしたつづきで、このクォータニオンのテストをしてみました。
参考: https://github.com/kynd/PQuaternion/blob/master/Quaternion.pde#L8
Processingのクォータニオンのクラスは上のものをそのまま引用させていただきました。
また、マウスドラッグ視点を変えられる便利なライブラリpeasyを使用しました。
http://mrfeinberg.com/peasycam/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import peasy.*; PeasyCam cam; int SZ = 600; void setup(){ size(600, 600, P3D); cam = new PeasyCam(this, 100); cam.setMinimumDistance(50); cam.setMaximumDistance(500); } void draw(){ background(240); for(int i=0;i<60;i++){ pushMatrix(); translate(i*10 - 300, SZ/2 - 300, SZ/2 -300); noStroke(); fill(255,0,0); sphere(2); popMatrix(); } for(int i=0;i<60;i++){ pushMatrix(); translate(SZ/2-300, i*10-300, SZ/2-300); noStroke(); fill(0,255,0); sphere(2); popMatrix(); } for(int i=0;i<60;i++){ pushMatrix(); translate(SZ/2-300, SZ/2-300, i*10-300); noStroke(); fill(0,0,255); sphere(2); popMatrix(); } pushMatrix(); translate(150, 150, 150); noStroke(); fill(0,255,255); sphere(4); popMatrix(); for(int i=0;i<60;i++){ pushMatrix(); Quaternion q = new Quaternion(); q.setAngleAxis(radians(15), new PVector(1, 0, 0)); PVector r = new PVector(SZ/2-300, SZ/2-300, i*10-300); PVector m = q.mult(r); translate(m.x, m.y, m.z); noStroke(); fill(255,0,255); sphere(1); popMatrix(); } } |
プログラムは、前回作成したプログラムからZ軸をX軸を中心に15度回転されせたものを上書きしました。(紫の点)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
public class Quaternion { public float x, y, z, w; public Quaternion() { x = y = z = 0; w = 1; } public Quaternion(float _x, float _y, float _z, float _w) { x = _x; y = _y; z = _z; w = _w; } public Quaternion(float angle, PVector axis) { setAngleAxis(angle, axis); } public Quaternion get() { return new Quaternion(x, y, z, w); } public Boolean equal(Quaternion q) { return x == q.x && y == q.y && z == q.z && w == q.w; } public void set(float _x, float _y, float _z, float _w) { x = _x; y = _y; z = _z; w = _w; } public void setAngleAxis(float angle, PVector axis) { axis.normalize(); float hcos = cos(angle / 2); float hsin = sin(angle / 2); w = hcos; x = axis.x * hsin; y = axis.y * hsin; z = axis.z * hsin; } public Quaternion conj() { Quaternion ret = new Quaternion(); ret.x = -x; ret.y = -y; ret.z = -z; ret.w = w; return ret; } public Quaternion mult(float r) { Quaternion ret = new Quaternion(); ret.x = x * r; ret.y = y * r; ret.z = z * r; ret.w = w * w; return ret; } public Quaternion mult(Quaternion q) { Quaternion ret = new Quaternion(); ret.x = q.w*x + q.x*w + q.y*z - q.z*y; ret.y = q.w*y - q.x*z + q.y*w + q.z*x; ret.z = q.w*z + q.x*y - q.y*x + q.z*w; ret.w = q.w*w - q.x*x - q.y*y - q.z*z; return ret; } public PVector mult(PVector v) { float px = (1 - 2 * y * y - 2 * z * z) * v.x + (2 * x * y - 2 * z * w) * v.y + (2 * x * z + 2 * y * w) * v.z; float py = (2 * x * y + 2 * z * w) * v.x + (1 - 2 * x * x - 2 * z * z) * v.y + (2 * y * z - 2 * x * w) * v.z; float pz = (2 * x * z - 2 * y * w) * v.x + (2 * y * z + 2 * x * w) * v.y + (1 - 2 * x * x - 2 * y * y) * v.z; return new PVector(px, py, pz); } public void normalize(){ float len = w*w + x*x + y*y + z*z; float factor = 1.0f / sqrt(len); x *= factor; y *= factor; z *= factor; w *= factor; } } |
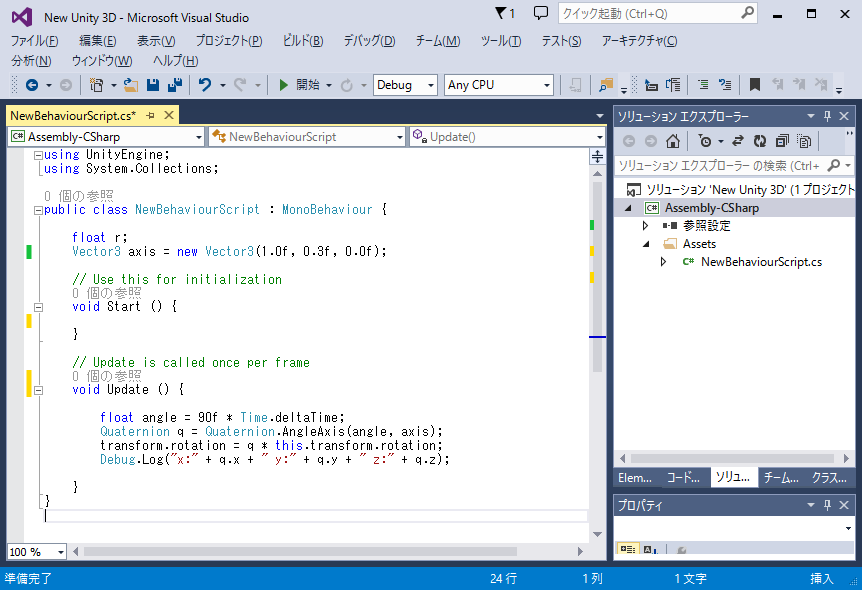
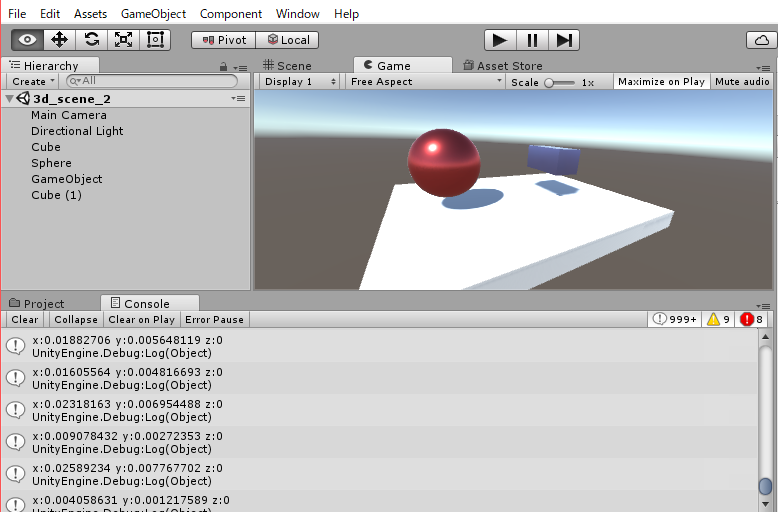
また以前、Unityを試したブログでこのQuaternionがでてくるので、ここでちょっとだけ復習してみました。
「Unity 5 / C#」
http://crossframe.iiv.jp/201611241241/
Categories: 未分類 タグ: Processing