GoogleのDeepLearningをはじめとする機会学習のライブラリがちょっと前に公開されました。まだわからないことばかりですが、少し使ったメモをしておきます。
まずインストールですが、Windowsマシンで使いたかったので、Dockerとともに使うことにしました。
環境: DockerToolbox-1.11.2.exe / Windows 10
WindowsのDockerでうまくいかなかった点は、以下を参考にしました。
https://caffinc.github.io/2015/11/tensorflow-windows/
コンテナを起動するとき、Image IDを指定します。
docker pull b.gcr.io/tensorflow/tensorflow
docker images
winpty docker run -it -p 8888:8888 [id]
今回、インタラクティブにコードを実行する環境のJupyter Nodebookをはじめて使いましたが(これまではiPython)、Dockerと合わせて使ってみて、これらとても便利です。
コンテナを立ち上げ、ブラウザでアクセスします。
192.168.99.100:8888/tree
Homeにある2_getting_started.ipynbをもとに編集しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 |
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt %matplotlib inline # Set up the data with a noisy linear relationship between X and Y. num_examples = 50 X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)]) X += np.random.randn(2, num_examples) x, y = X x_with_bias = np.array([(1., a) for a in x]).astype(np.float32) plt.figure(figsize=(4,4)) plt.scatter(X[0], X[1]) plt.show() # Keep track of the loss at each iteration so we can chart it later losses = [] # How many iterations to run our training training_steps = 50 # The learning rate. Also known has the step size. This changes how far # we move down the gradient toward lower error at each step. Too large # jumps risk inaccuracy, too small slow the learning. with tf.Session() as sess: # Set up all the tensors, variables, and operations. input = tf.constant(x_with_bias) target = tf.constant(np.transpose([y]).astype(np.float32)) weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1)) tf.initialize_all_variables().run() yhat = tf.matmul(input, weights) yerror = tf.sub(yhat, target) loss = tf.reduce_mean(tf.nn.l2_loss(yerror)) update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) for _ in range(training_steps): # Repeatedly run the operations, updating the TensorFlow variable. update_weights.run() #sess.run(update_weights) #losses.append(loss.eval()) losses.append(sess.run(loss)) # Training is done, get the final values for the graphs #betas = weights.eval() betas = sess.run(weights) #yhat = yhat.eval() yhat = sess.run(yhat) # Show the fit and the loss over time. fig, (ax1, ax2) = plt.subplots(1, 2) plt.subplots_adjust(wspace=.3) fig.set_size_inches(10, 4) ax1.scatter(x, y, alpha=.7) ax1.scatter(x, np.transpose(yhat)[0], c="g", alpha=.6) line_x_range = (-4, 6) ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], "g", alpha=0.6) ax2.plot(range(0, training_steps), losses) ax2.set_ylabel("Loss") ax2.set_xlabel("Training steps") plt.show() losses = [] training_steps = 10 learning_rate = 0.002 with tf.Session() as sess: input = tf.constant(x_with_bias) target = tf.constant(np.transpose([y]).astype(np.float32)) weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1)) tf.initialize_all_variables().run() yhat = tf.matmul(input, weights) yerror = tf.sub(yhat, target) loss = tf.reduce_mean(tf.nn.l2_loss(yerror)) update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) for _ in range(training_steps): update_weights.run() losses.append(sess.run(loss)) betas = sess.run(weights) yhat = sess.run(yhat) fig, (ax3, ax4) = plt.subplots(1, 2) plt.subplots_adjust(wspace=.3) fig.set_size_inches(10, 4) ax3.scatter(x, y, alpha=.7) ax3.scatter(x, np.transpose(yhat)[0], c="g", alpha=.6) line_x_range = (-4, 6) ax3.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], "g", alpha=0.6) ax4.plot(range(0, training_steps), losses) ax4.set_ylabel("Loss") ax4.set_xlabel("Training steps") plt.show() |
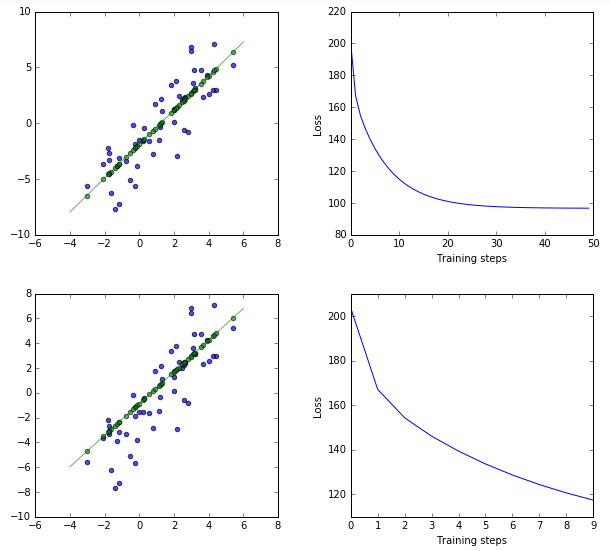
同じ初期値を使って違うパラメータでテストをしたかったので、あまりいいやり方ではないのですが、処理を2回記述しています。また同じ意味になるようなので、わかりやすくするためsessを使った書き方にしてみました。
直線を元にした50個の点データのx座標を乱数でちらしたデータのx,yの関係を学習して、最終的に緑色の点を計算して描画するものです。
パラメータによる傾きの違いを確認しました。
この環境いいかも・・
とりあえずここまでメモでした。