微分方程式の解を求めるOctaveのlsode関数を使って、微分方程式の復習と、任意データへの適用を試みてみました。

function ydot = f1(y, t)
	ydot = -y;
endfunction

t = linspace(0, 10, 100);
y = lsode("f1", 1, t);
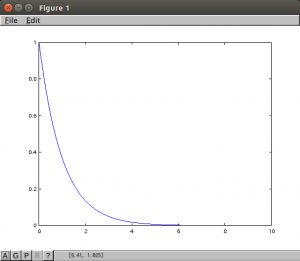
plot(t, y)           #1
plot(t, exp(-t))     #1

plot(t, f1(t, 0))    #2

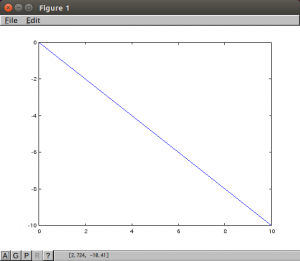
まずシンプルな微分方程式の解をプロットしてみました。
#1の一つ目は、lsodeで解いたもの、二つ目は、式で解いたものをですが、同じものになることを確認しました。

dy/dt = -y
1/y dy = -1 dt
log y = -t + C
y = K exp(-t) (t=0, y=1)

式はこのように解き、#2も一応確認しました。

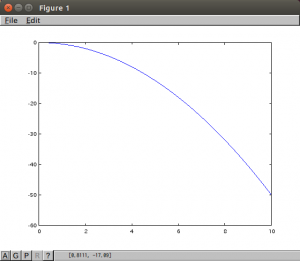
tについての微分も試してみました。

function ydot = f2(y, t)
	ydot = -t;
endfunction

y = lsode("f2", 0, t);
plot(t, y)                  #3
plot(t, -1 / 2 .* t .* t)   #3

plot(t, f2(0, t)); #2

#2はf1のときと同じになります。

y= – 1/2 t^2
dy/dx = -t

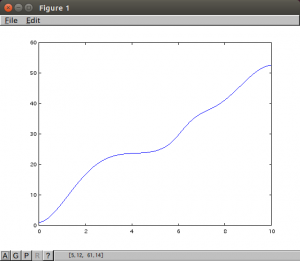
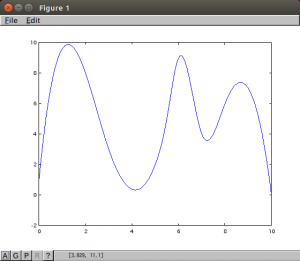
次が今回やりたかった任意の離散データを対象にしてみました。

function ydot = f3(y, t)
	x1=[0 2 3 5 5.5 6 7 8 9 10];
	y1=[1 8 3 2 5   9 4 6 7 0];

	ydot = spline(x1,y1,t)
endfunction

y = lsode("f3", 1, t);
plot(t, y) #4
plot(t, f3(1, t)); #5

splineを使い、連続関数のようにしてテストしてみました。

#4

#5

適当につくったデータですが#5を積分すると#4、なんとなくイメージできます。しかしspline関数、なかなか綺麗に描いてくれますね。

あと、便宜上関数定義を他と同じ個所に書いていますが、Mファイルに同名ファイル(例 f1.m)を作って、別コンソールでエディタを開き編集しながらテストすると、便利です。