Posted on 2014/06/15, 12:22 AM By admin22
ベイズ統計にでてくる尤度関数について、まとめておきたいと思い書きました。
その前にある区間の最大値、最小値を求めるRの関数についてのテストです。
|
1 2 3 4 5 6 7 8 |
par(col.axis='firebrick2', col.lab='white', bg='gray33', fg='white') f <- function(x){x^3+(x-1)^2} x = seq(-2,2,length=201) t1 <- optimize(f, c(-2,0), maximum=TRUE) t2 <- optimize(f, c(-1,2), maximum=FALSE) plot(x,f(x), col=7, type='l') abline(v=t1$maximum, col=4) abline(v=t2$minimum, col=4) |
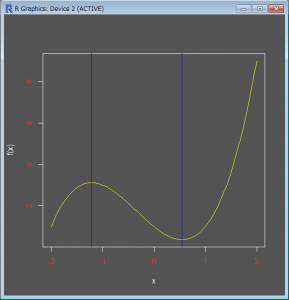
三次関数の極大値、極小値を図示しています。optimizeを使うと、指定区間のこのような値を求めてくれます。
そして、尤度関数についても、最大値を求めてみます。
|
1 2 3 4 5 |
L <- function(p){p^3*(1-p)^7} p <- seq(0,1, length=101) t3 <- optimize(L, c(0, 1), maximum=TRUE) plot(p, L(p), col=7, type='l') abline(v=t3$maximum, col=4) |
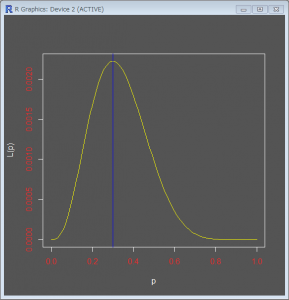
この試行は、コインを10回投げて、3回表がでたと想定します。
尤度関数が最大となる0.3が表がでる確率を表しています。
最大値は、モード(最尤値)として以下のようにも計算できます。
((3+1)-1)/((3+1)+(7+1)-2) = 0.3
このp^n(1-p)^nは、ベータ分布(ベルヌーイ分布)と呼ばれ、関数にしてみました。(係数は簡略化しています)
|
1 2 3 4 5 |
Beta <- function(x, a, b){x^a*(1-x)^b} par(mfrow = c(3,1)) plot(p, Beta(p, 0, 0), col=7, type='l') plot(p, Beta(p, 1, 1), col=7, type='l') plot(p, Beta(p, 2, 0), col=7, type='l') |
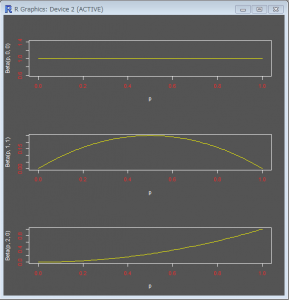
一番上は、一様分布を表します。
Beta関数の第二引数、第三引数は、上の例で言えば、表が出た回数と裏が出た回数に相当します。
そして三番目の分布を事前分布として、尤度をかけて事後分布をもとめると以下のようになります。
|
1 2 3 |
par(mfrow = c(2,1)) plot(p, Beta(p, 2, 0) * L(p), col=7, type='l') plot(p, Beta(p, 2, 0) * L(p) * L(p), col=7, type='l') |
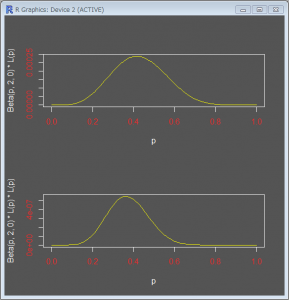
事後分布を事前分布に更新(ベイズ更新)して繰り返し尤度をかけていくやり方は、マルコフの状態遷移行列にも似てるように感じました。
Categories: 未分類 タグ: R
