Posted on 2014/05/25, 10:41 AM By admin22
Rのnls関数を使った非線形回帰分析をテストしていて、これを使うまでもない簡単なケースで、直感的にできる方法を試してみました。
環境: R version 3.0 / Windows 7
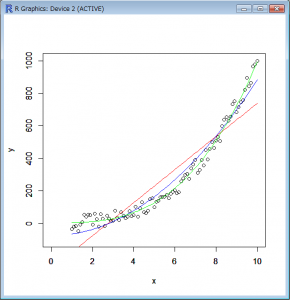
対象のデータは、三次曲線にノイズを負荷して、散らしたものを使いました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
x=seq(1,10,0.1) y=jitter(x^3,amount=50) df = data.frame(x,y) f1 <- function(data,par) with(data, sum((par[1] + par[2] * x - y) ^ 2)) f2 <- function(data,par) with(data, sum((par[1] + par[2] * x ^ 2 - y) ^ 2)) f3 <- function(data,par) with(data, sum((par[1] + par[2] * x ^ 3 - y) ^ 2)) res1 <- optim(par = c(0,1), f1, data = df) res2 <- optim(par = c(0,1), f2, data = df) res3 <- optim(par = c(0,1), f3, data = df) plot(df, xlim=c(0, 10), ylim=c(-100,1000), ylab='y'); par(new='T');plot(x,res1$par[1] + res1$par[2] * x, type='l', col='red', xlim=c(0, 10), ylim=c(-100,1000), ylab='y') par(new='T');plot(x,res2$par[1] + res2$par[2] * x ^ 2, type='l', col='blue', xlim=c(0, 10), ylim=c(-100,1000), ylab='y') par(new='T');plot(x,res3$par[1] + res3$par[2] * x ^ 3, type='l', col='green', xlim=c(0, 10), ylim=c(-100,1000), ylab='y') |
一次、二次、三次それぞれについてデータにフィッテングさせてみます。
これは「関数」に対して最適な係数を探し出すものでとても強力で興味深い機能です。
(元のデータをグラフで見て、適用できそうな関数を選ぶ)
参考サイト:
How to use optim in R
Categories: 未分類 タグ: R