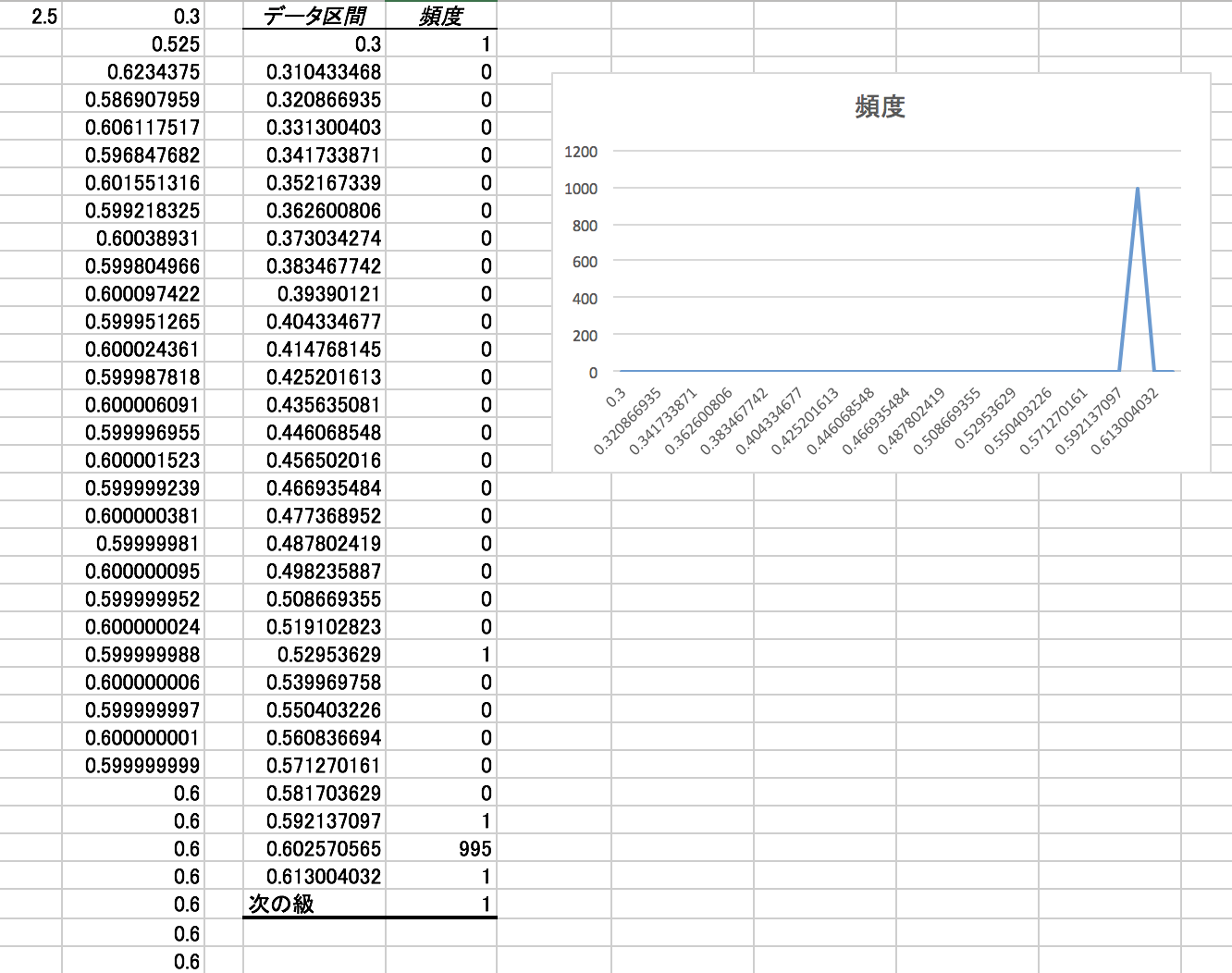
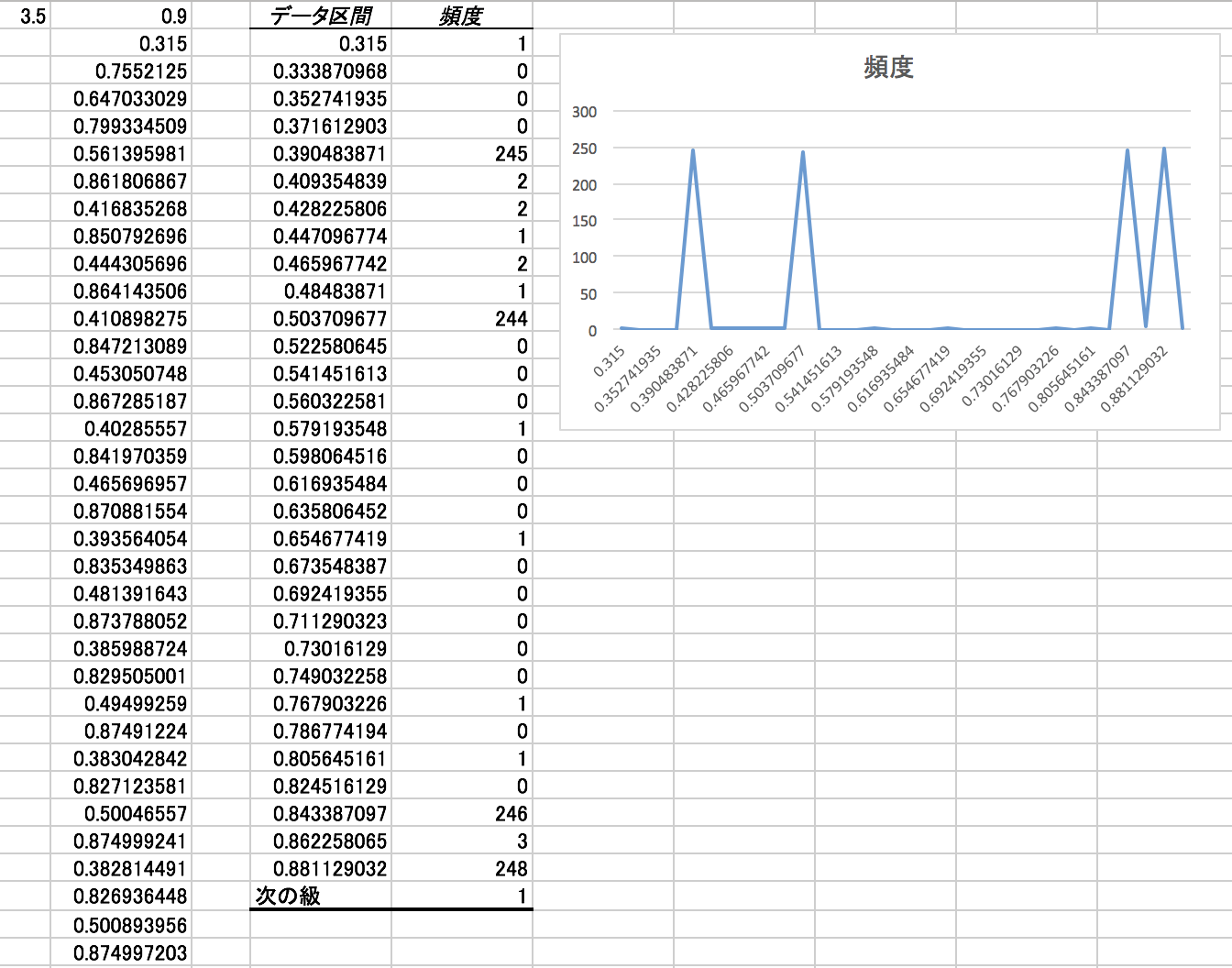
離散型ロジスティック方程式とよばれる漸化式X{n+1} = a * X{n} * (1 – X{n}) 。
シンプルな式なのに、定数aの値により、収束したり周期的になったり全く予想しない値になったり多様な振る舞いをします。
30年以上前の本になりますが、山口昌哉氏の「カオスとフラクタル〜非線形の不思議」(ブルーバックス)で初めて知りました。たぶんこの部類の本の中では一番解りやすいのではと思います。同じ時期に読んだ武者利光氏の「ゆらぎの世界」(ブルーバックス)とともにとても影響をうけました。(これら両書とも説明が丁寧で親切なのが特徴です)
ゆらぎについては、下記プログでも。
決定論的なのにランダムと区別がつかない数列をつくることができるので、毎回同じ振る舞いをする乱数?としてアルゴリズム作曲などに使ったこともあります。(擬似乱数もシードが同じなら同様の振る舞いをしますが、プラットホームが違っても同じ値を使いたいときとか、乱数としての性能は専用ロジックにはかなわないが、演算プロセスをわかりやすいものにしたいときなど有用)
決定論とランダム、最近話題のユヴァル・ノア・ハラリ氏の「ホモ・デウス」の中でもたびたび出てくるキーワードですが、現在でも必須のアイテムではないでしょうか。
0<=a<=1: 0に収束
1<a<=2: 1-1/aに収束
2<a<=3: 1-1/aに振動して収束
3<a<=1+sqrt(6) : 周期2
1+sqrt(6)<a<=3.5699456.. : 周期4,8,16..
3.5699456..<a<=4: 収束も周期性もない複雑な挙動
一部をExcelでテスト
A1: 定数a
B1: 初期値X{0}
B2: =$A$1*(1-B1)*B1
B3:=$A$1*(1-B2)*B2
B4..以下同様 データ数1000
aを面白くなってくる3.0から0.1ステップで4.0まで3Dで表示してみました。
Frequency関数でデータ配列上と同様1000、区間配列は0.01ステップで100で計算(0から1)
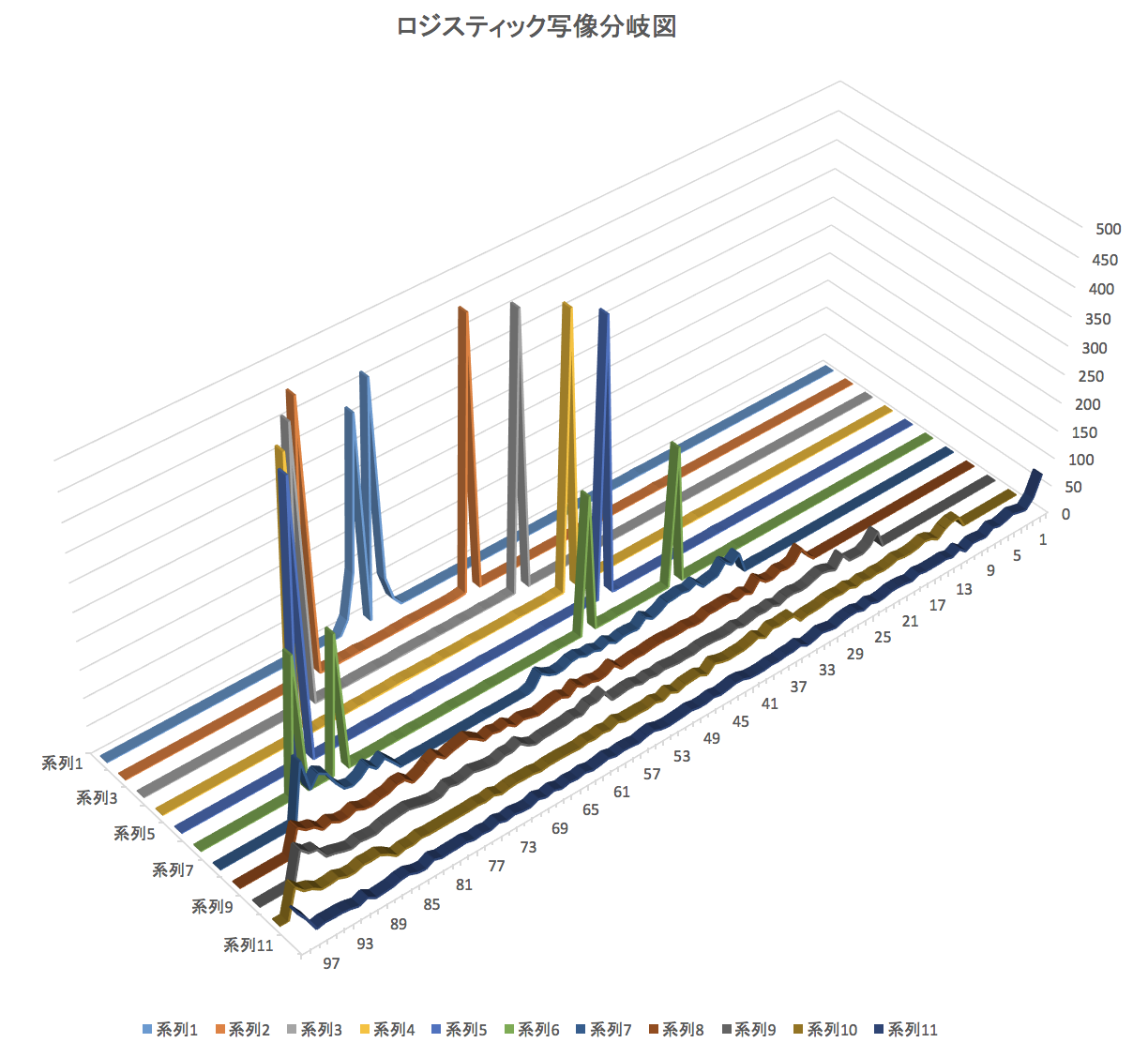
3.6 あたりから複雑になり、4では全ての区間で値が存在して両端が多いですがほぼランダムと同じくらいの頻度となります。
ウィキペディアにある図と比べるといい感じになっていることがわかると思います。
https://ja.wikipedia.org/wiki/%E3%83%AD%E3%82%B8%E3%82%B9%E3%83%86%E3%82%A3%E3%83%83%E3%82%AF%E5%86%99%E5%83%8F